快速排序

快速排序的原理

快速排序算法是将数组按序不断分解，直到所有子数组不能再分，那么所有子数组拼接起来就是一个完整的有序数组。
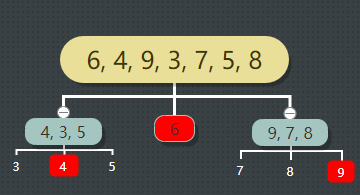
首先，从数组中选取一个数作为基准值，比这个基准值小的元素放在左边，大的放在右边。然后对左右两个新数组继续进行上述步骤，直到所有的子序列只剩下一个元素。如下图（图中取数组第一个元素作为基准值）:

快速排序的实现

使用Javascript实现:

//方法1
const quickSort = (array) => {
  const sort = (arr, left = 0, right = arr.length - 1) => {
    if (left >= right) {//左边的索引大于等于右边的索引则表示不能继续分解
      return;
    }
    let i = left;
    let j = right;
    const pivot = arr[left]; // 取无序数组第一个数为基准值
    while (i < j) { //把所有比基准值小的数放在左边 大的数放在右边
      while (j > i && arr[j] >= pivot) { //从右向左找一个小于基准值的元素
        j--;
      }
      arr[i] = arr[j]; //将较小的值放在当前i的位置 没找到的情况下i 等于 j
      while (i < j && arr[i] <= pivot) { //从左向右找大于基准值的元素
        i++;
      }
      arr[j] = arr[i]; // 将较大的值放在当前j的位置 没找到的情况下i 等于 j
    }
    arr[i] = pivot; // 将基准值放至i位置完成一次循环（这时候 j 等于 i ）
    sort(arr, left, j - 1); // 将左边的无序数组重复上面的操作
    sort(arr, j + 1, right); // 将右边的无序数组重复上面的操作
  };
  sort(array);
  return array;
}

这段代码是不是感觉很难读懂，尤其是在数组元素交换的过程。那么下面这个版本更好理解:

//方法2
const quickSort1 = function(arr) {
  if (arr.length <= 1) { //如果数组长度小于等于1无需继续分解
    return arr;
  }
  const pivot = arr.shift(); //取基准值的值
  const left = []; //存放比基准值小的数组
  const right = []; //存放比基准值大的数组
  for (let i = 0; i < arr.length; i++){ //遍历数组，进行判断分配
    if (arr[i] < pivot) {
      left.push(arr[i]); //比基准值小的放在左边数组
    } else {
      right.push(arr[i]); //比基准值大的放在右边数组
    }
  }
  //递归执行以上操作,对左右两个数组进行操作，直到数组长度为<=1
  return quickSort1(left).concat([pivot], quickSort1(right));
};

上述代码就清晰多了，这段代码很清晰的展示了快速排序的过程，不过也是有代价的，因为每次递归都创建了新的数组，所以运行时内存的需求也就更大。
使用ES6的rest语法的实现：

//方法3
const quickSort2=([head,...tail])=> head===undefined ? []
  : quickSort2(tail.filter(a=>a<head))
    .concat(head)
    .concat(quickSort2(tail.filter(a=>a>=head)));

使用函数式编程工具库Ramda实现的快速排序：

//方法4
const R = require('ramda');
const quickSort3 = R.unless(        //直到返回空数组长度为1停止递归
  arr=>R.length(arr)<=1,
  ([pivot, ...rest]) => [
    ...R.compose(quickSort3, R.filter(R.lt(R.__, pivot)))(rest), //比基准值小的放到左边
    pivot,
    ...R.compose(quickSort3, R.filter(R.gte(R.__, pivot)))(rest), //大于等于基准值的放到右边
  ]
);

性能测试

上面几种写法的性能怎样呢？写段代码测试一下吧，先生成一个长度10000随机数组:

function genDisorderArray( len ){
  let result = [];
  for (let i = 0; i < len ; i++) {
    result.push( (Math.random()*len)>>0 );
  }
  return result;
}

const randomArray = genDisorderArray( 10000 );

使用一个循环执行10遍排序代码，计算时间:

console.time("quick sort");
for (let i = 0; i < 10 ; i++) {
  quickSort(randomArray);
}
console.timeEnd("quick ramda");

结果：

方法1：14ms
方法2：35ms
方法3: 199ms
方法4: 810ms

不同的实现性能相差这么多，尤其是方法3和方法4，虽然写法简洁，但是性能能却差了些。仔细分析一下，方法3和方法4在使用filter方法时实际上多进行了一次循环，那么优化一下呢?

//方法5
const quickSort4 = R.unless(        //直到返回空数组长度为1停止递归
  arr => R.length(arr) <= 1,
  ([pivot, ...rest]) => R.compose(
    ({left = [], right = []}) => [...quickSort4(left), pivot, ...quickSort4(right)],
    R.groupBy((val) => R.gt(val, pivot) ? "right" : "left")
  )(rest)
);

测试之后结果：408ms，效率依然很低。

以上对快速排序算法的研究更多的是关注代码的实现，通过代码的实现来理解快速排序的原理。

时间复杂度

平均状况下时间复杂度为O(n log(n)), 最坏情况下时间复杂度为O(n²)

总结

快速排序是需要借助于递归来实现的，在函数为返回结果前前嵌套调用会在当前调用帧里再次嵌套调用帧，递归的不断嵌套会导致会导致堆栈溢出，当然这是要在数据量超大的情况下才会发生。针对递归堆栈溢出的解决办法就是使用尾递归优化，遗憾的是快速排序是无法使用尾递归的，因为快速排序在函数return时需要对左右两段序列进行递归排序再合并的操作。上文所举实例中第一个算法的效率是最高的，其他几种写法只是为了方便理解快速排序。另外ramda是一个很好的函数式工具库，不过实现的快速排序却是效率最低的，仅作参考。